Remote Mathematicians

In this "new world" of remote learning, keeping students engaged in content can seem daunting. That feeling of not just sharing content, but making it easily accessible and engaging enough for students to stay connected, brings its challenges.
As a previous math teacher, it was tough enough helping students enjoy the content, so flexing the "creativity" muscle in the brain was a CONSTANT.

During this time, I thought I'd share my top 3 go-to strategies!

TIP #1: Encourage inquiry and self-discovery!

• Geogebra: This site offers Classroom Resources from elementary up to college courses. Students can explore theorems, visualize multiple cases, and then easily develop their proof. Geogebra even has built in activities with self-checks. Follow Tim or Steve on Twitter to see their creations.
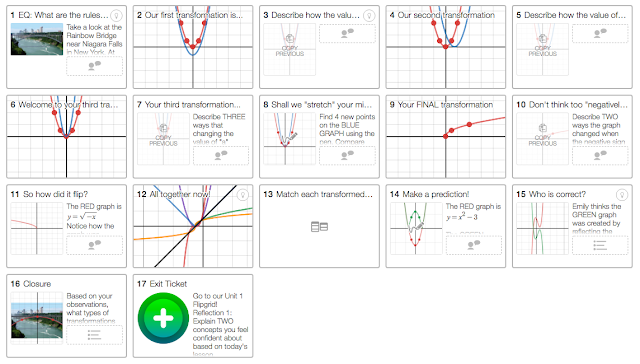
• Desmos: Teachers can create a FREE account and send activities to their students. Use one that's already made or create your own! Explore transformations and how variables can affect equations.
• NEW UPDATE ALERT: Add a co-teacher!
• NEW UPDATE ALERT: Send customized feedback to students.

TIP #2: Increase the open dialogue by using open tasks!

• Which One Doesn't Belong: 4 boxes...which one doesn't belong? The best part - there is a reason EVERY SINGLE ONE doesn't belong. Bring the discussion into math and allow students to see there isn't just "one answer." Do you have gifted students? Encourage them to create their own!

• Copy/paste a puzzle and use THESE SLIDES! Share it with students so everyone can edit the same file. 
• Numbers Example (for Elementary up to High School)
• Open Middle Math: One problem can completely replace a worksheet! Students not only practice, but must use logic and reasoning to finish the puzzle. Available for K-12 students!
• PRO TIP: Share on a Google Slides or Keynote for students to respond. They can drop in recording to explain their thinking.
• PRO TIP: Use master slides to create text and image placeholders for students.
• PRO TIP: Attach an Open Middle or WODB problem to the "Focus" in a Flipgrid Topic. Ss can use the whiteboard mode to share their thinking with their peers! 

TIP #3: Using the tech in your tool belt!

• Keynote (on the iPad): While it is similar to Google Slides, Keynote on the iPad takes the advantage! A fantastic mathematician and edtech enthusiast, Morgan Cave, on the team I work on got me into this app, and there is NO turning back! As an Apple Distinguish Educator, she's continuing to push outside the box for how Keynote can be used to explore all concepts.
• Built in shapes (including 3D ones with the latest iOS update!)
• Drop in just audio to explain thinking.
• Utilize the Drawings option with multiple colors to clarify steps. My favorite? Use the "Line Draw" animation so that students can visualize their work (and steps) come to LIFE!
• Use backgrounds and "locking" to prevent students editing important information.
• Templates from Morgan Cave: Shapes Hunt, Alpha See Say Draw, Numbers See Say Draw
• $FREE Apple Books: 20 Keynote Creations & Keynote in the Classroom
• Google Slides (for Chromebook): 
• Use master slides to create template responses with placeholders.
• Ss can drop in pictures, links, videos, text, animations, and MORE all in one place.
• Collaboration feature for discussions or group work is PERFECT! With the editing history, no work is lost and students are help accountable for their contribution.
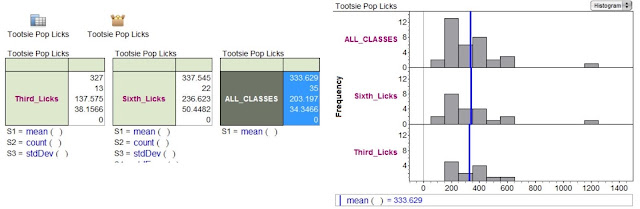
• Google Sheets (for Chromebook): Check out these helpful resources and templates using the "ugly step sister" of the G-Suite family!
• Eric Curts' Blog
• Create a digital breakout activity with if-then formulas!
• Math Learning Apps:
• Digital manipulatives for the WIN!
• 100% FREE!
• Includes annotation feature! 
• PRO TIP: Ss can screenshot their creation, and drop it in Seesaw or Keynote to add audio!
• Flipgrid:
• Whiteboard Mode = PERFECT for explaining work.
• Drop in a video, picture, and/or links in the Focus for your Topic.
• Students don't want others to see their face? Use Pixel Mode!
• Check out their Disco Library for Topics ready to go!

Navigating the Course

As I finished up Teach Like a Pirate by Dave Burgess, I found myself evaluating my previous lessons and how I used the hooks he mentioned and how I could improve the ones that needed what he calls "seasoning".

The lesson that I want to share is a topic in PreCalculus (used to be taught in Algebra 2) called Conic Sections. If you've ever taught it, you know it can be a beat down for students, causing (pun intended) circles to go around their head, which I find such a shame because it was my FAVORITE to teach.

All students love Play Doh!
(It really is the little things in life)

I loved how changing just a few numbers could affect the graph so drastically yet they were all related to each other in the smallest ways. I enjoyed that I could find all of them by simply slicing a cone differently at various angles. (The intro lesson I use for this unit involves students molding Play-Doh into a cone and using floss to make the various cross sections...yes, high school students go NUTS for Play-Doh!) The best part about this unit? It's usually BRAND NEW to students and I get to be the one who shares it! To watch them ask questions, and say "Oh don't you worry...that's tomorrow's adventure!" and "I love that you connected those ideas. Share that with your group, and if you'd like, with the whole class!" While the formulas can be a bit dull, it's the relationship between the equations that I find the most intriguing - and more importantly, the hidden applications they offer! One of the more interesting applications is to the medical field - whaaa?!?!

The lesson in particular that I enjoyed the most was about ellipses - the elongated circle if you will. I used a variety of Dave's hooks throughout and added some improvements so that teachers who were 1:1 could see how to integrate more technology! Although the hooks didn't really change the content, it made the presentation stronger and students were eager to learn - isn't that what we want?

Google Slides Exit Ticket

The "Hooks": Because the application I chose involved the medical field, all my hooks revolved around that!

• The Mozart Hook: As students were walking in, I had the theme song for Dr. House playing - "Teardrop" by Massive Attack
• The Picasso Hook: Students were given a half-sheet where they connected the intersection of the curves to make an "oval" shape. When they were finished, they measured various distances to discover the definition of an ellipse. You can also do this with wax paper using these directions.
• The Real World Hook: As an extension for that evening, students read up about one application of ellipses (lithotripsy - the process of dissolving kidney stones), solved the problem using the Chrome extension, and then had to find another application online. Curious about the application in further detail? Check out this site!
• The Costume Hook: A dressed up in purple (my school color) scrubs for the entire day.
• The Techno Whiz Hook (New Addition): As mentioned above in the "Real World" Hook, students solve a problem and did further investigating. Instead of doing this on paper and turning it in, they shared their thinking and solving on a collaborative Google Slides and their applications on a Flipgrid (WHICH IS FREE NOW!) 

The Challenge

Could there be even more hooks to include? Absolutely! I must say that when I was reading his book, I found some hooks were challenging for math, but had to ask myself, isn't that good?! I can re-imagine my lessons, re-think some strategies, and will encourage me to utilize the strengths of my team! How energizing, am I right?! Instead of teaching the same lesson, I get to "take the stage" with the content.

One of my favorite parts of his book was that it was content-neutral. He stresses that ANYONE with ANY CONTENT can teach using the P.I.R.A.T.E method if they just begin with an open-mind and a willingness to step outside of their comfort zone. He emphasizes that not every lesson will be success - some might even FAIL! And the biggest kicker - that it's OKAY! You get to try again the next day and even the day after that. I know I've had lessons that have fallen flat, and while discouraging at first, it lets my students see how I respond and how they too can respond when things don't work the first time. If it doesn't work, then it's feedback time! Isn't that a valuable lesson even if it's not content related?

A "functional" Transformation

One of the biggest topics in a secondary mathematics class is function transformations (horizontal/vertical shift, compressions, stretches, etc.) Usually students will memorize the rules rather than understand the reasoning. I needed a way to enhance the lesson to allow students room to investigate these concepts and draw their own connections and conclusions - time to spice things up with technology!

Topic: Intro to Transformations

Essential Question: How can I transform ANY function?

Materials:

• Desmos Activity - Make a copy if you'd like to make some adjustments! (link)
• Student Notes - Google Slides (link) Click [Use Template] to make your own copy in your Google Drive.
• 1 device per 2 students - I recommend a Chromebook/computer.
• Recommendation: a Google Classroom to share the notes with each student.

Student Notes (Google Slides) Preview

Teacher Notes:

1. Assign the notes in Google Classroom where each student gets a copy.
2. Go to teacher.desmos.com. If you don't have one, create an account! I recommend with a Google Account to make the sign-in easier.
3. Open the Desmos Activity (Intro to Transformations) above. 
4. Click on the teal [Create Class Code]. This will need to be copied on Slide 1 in the Google Slides. This is how students will access the activity.

   

   Desmos Activity (Preview)

5. Students will partner up and bring their computer/Chromebook. Each student can login so that everyone answers the activity questions and can take screenshots to add to their Google Slides for their notes.
6. Encourage students to take their time exploring each transformation carefully. They may struggle understanding shifting left and right. I related it back to the distance formula - (x - 3) moves RIGHT 3, not LEFT. 
   
7. The Exit Ticket/Reflection piece is on Flipgrid. Create a TOPIC in Flipgrid where students can respond.
8. TIP: I created a topic for EACH UNIT in my class so that students could see how their questions and reasoning improved as the unit continued. 

My Reflection:

• Since the remaining of the year (and future mathematics courses) depended on this lesson, I felt strongly about student exploring it on their own. I tried teaching the rules one year and it only set them up for failure later. 
• I'm currently reading Shake Up Learning by the infamous Kasey Bell of Texas. In her first couple of chapters, she stresses the importance of integrating 21st century skills into as many lessons as possible - hence, shake things up! Students will be asked to analyze critically and shoving rules in their faces wasn't accomplishing this and was NOT preparing my students for their future careers. Careers where thinking on their own and creating their own connections would be a requirement.
• One of my biggest fears with "shaking up their learning" is that my students won't learn the concepts "correctly". What if they misunderstand and I don't catch it?! In my mind, technology allows me to assess formatively more often, therefore I can check understanding frequently. When my concern of "learning incorrectly" snuck in to my mind, I forced myself to remember Jo Boaler - making mistakes is a learning opportunity. Even more so, making mistakes will make their brains grow. 

So how many licks...?

Everyone knows the famous question that's plagued children and adults for millenia...

How many licks does it take to get to the tootsie center of a Tootsie Pop?

One of my absolute favorite lessons in AP Statistics was the Tootsie Pop Lab. This lab emphasizes how to estimate the ACTUAL average amount of licks it takes to get to the center. Will this question ever be answered!? Non-Statisticians would tell you "nah", but the real Statisticians would use inference mathematics. In this realm, we can get pretty close to the actual answer by providing a range of possible answers that could be true - what Statisticians call a Confidence Interval.  

A big idea running through the veins of Statistics is the idea of an unknown parameter - the ACTUAL population value. Example questions we could answer that have these unknown parameters would be...

1. What proportion of the world is covered in water?
2. What is the average life expectancy in the United States?
3. What is the average number of books teens read?

Clearly they were into it!

Clearly, it would be a challenge to find the ACTUAL percentage of the world covered in water or the actual average life expectancy, but we can get reallllllly close by taking sample measurements and drawing conclusions from there - i.e. finding a statistic! 

In Statistics, it's about getting on the dart board - not the bull's eye!

This lab teaches students this very idea! We may never really know the answer, and THAT'S OKAY! Using inference to draw conclusions is what mathematics can yield - and even better, we can provide plausible answers! It's a rare glimpse into the power and insight that only mathematics can provide. 

Activity: Tootsie Pop Lab

Essential Question: 

How can I estimate the true average amount of licks it takes to get to the center of a Tootsie Pop?

Materials:

• Tootsie Pop Presentation - Google Slides (click Use Template for your own copy!)
• Tootsie Pop Analysis - Padlet (click Remake if you want to use it!)
• Student Notes - Google Sheet (click [Make a Copy] and now it's in your Drive!)
• Flipgrid - create 1 topic in Flipgrid where students can post their reflection asnwers

Possible Student Google Sheet

Provide students with the directions about licking their lollipop and remind them to lick in the SAME SPOT. You'd be surprised how into it your students get. I recommend putting them in partners, especially if you have a student who doesn't like lollipops.

As students begin to find their center, have each student enter in their number of licks on the Google Sheet. I highly recommend using Google Classroom to help you share information with students. You'll be sharing the Sheet, Flipgrid, and Padlet with them.

Teacher Presentation (other slides included)

PRO TIP: In Google Sheets, type "=" to get the formulas to work. For example, "=average(...)" and then students can select all the trials at once. It works similarly for the others.

Take-Aways:

• The "homework" for the evening is not practice problems at all! It's all about reflecting on what they discovered in class. Students recalled previous information to see how it fits in to their new content.
• Students LOVE candy (surprised about that?)
• Students enjoyed working with REAL DATA! It's not made-up numbers from a textbook or internet. It was personal. They were the data.
• Putting them in partners helped them find formulas in Google Sheets quickly and allowed them to process their ideas out loud.
• Why I used Padlet: helps students collaborate all at once in an easy way. Students can add voice notes, drawings, text, links, and photos for everyone in the class to see. This allows students to express their learning in a variety of ways that best fits them.
• Why I use Flipgrid: Students can post their reflection questions after the lessons and hopefully hear from other students. This way, students can respond to each others questions and really utilize peer feedback. This develops a community in the classroom, because we are all learning together.

Interested in the answer my students found? Check it out!

Before my district had Chromebooks for every student, I used Fathom to gather all of the data from my classes last year. Here is what we've discovered!

My students were really surprised that both classes had an average close to 330 licks.

Our Class Average amount of licks: 333.629 licks

My Class Data (2016)

A New Mindset

In one of my book studies that I'm participating in, I'm forced to reconsider the way mathematics is approached in the classroom. Dr. Jo Boaler is a professor at Stanford University for Mathematics Education. Her passion involves helping math teachers ACTUALLY TEACH mathematics. She strives to encourage teachers to move away from "sit and get" styles to pattern-investigation methods.

"When textbooks introduce only the simplest version of an idea, students are denied the opportunity to learn what the idea really is." Dr. Jo Boaler from Stanford University

What I'm reading

She is breaking down the wall and suggesting new, innovative ways to improve EVERY student's success in maths. She does not support the idea that you have a "maths" brain. She explores various research studies that show any student can learn maths if taught using some of her strategies which can include:

• Show examples and non-examples of definitions
• Rethink homework assignments to be reflection based instead of problem based
• Have students explore different methods and compare and contrast
• To reinforce concepts, have students use the concepts in different ways
• NO memorization - but utilize BOTH sides of the brain
• REMOVE timed-testing and math facts

I know what you're thinking...how can I do this? How can students learn maths if I don't show them the best methods and those precious shortcuts?! 

One of my toughest lessons in Algebra was Completing the Square. Students didn't understand for one thing, why it was even called that! They couldn't remember "all the steps" and couldn't make a connection what was really happening. Students memorized the steps and continued on their year which eventually lead to a brain dump to make room for the next memorization event.

Jo discusses the idea of "compression" in our brains. She explains, "when you learn a new area of mathematics...it takes up a large space in your brain." Once you play with ideas and dig deep, you can "file" them away and "compress" them. My biggest "Ah-ha!" moment was when she states, "Notably, the brain can only compress concepts; it cannot compress rules and methods." 

This allowed me to re-create my lesson on Completing the Square utilizing Algebra Tiles to help students explore the concept and build their own connections. If you've never used Algebra Tiles, I HIGHLY recommend it.

Student Notes (Google Slides)

Students build the polynomial using the tiles to literally make a square and determine how many 1's would it take to "complete" it. Throughout the process, students are reflecting on their learning and creating their own solving steps. For the extension exercise (i.e. homework), they will discover the Quadratic Formula! WHAAAA?!!?! Additionally, they will respond on a Flipgrid about their learning.

Student Reflection assignment

Materials:

• Notes: Complete the Square (1 copy for each student) - Google Slides
• Khan Academy Video (already in slides)
• Flipgrid: Create a Quadratics Topic for students to post their thinking
• Bitmoji: Students add bitmojis on their exercises to show how they feel

My Take-Away: 

Every student felt successful learning this new method. I had students make connections to other topics (graphing quadratics using the vertex) and even preferred this method OVER factoring! I couldn't believe the positive energy that was occurring and for once, the students were the ones doing the thinking! I became a guide for the day and my students didn't feel the need to have 20 identical problems for homework. 

Questions you could ask them for reflection exercises (consider using Flipgrid):

1. What kind of number for "b" makes completing the square easier? Explain your thinking.
2. What do you think would happen if "a" is not 1?
3. Do you think this method could work every single time? Defend your position.
4. Is there a time that this method works better than another? Explain by creating your own example.
5. Compare this method with factoring.